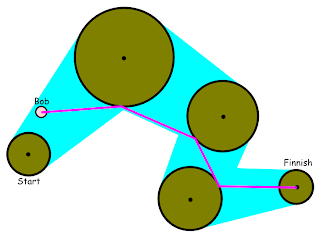
You have a bunch of Nav-Circles all set up neatly on a map, but all you can see are the circles.
Indeed drawing circles on a computer screen is only a small jump and a bit of maths from drawing a triangle so that need not be the issue, the issue is what you should see between the circles. If you look at my previous examples (and the one below) you will no doubt notice that all the walk-able areas are draw (in Inkscape's beautiful list of default colours), and that was pretty easy doing it all by hand.
I naively figured that it would be pretty simple to get the computer to do the same; all the information's there, it's just a bit of vector maths, how hard could it be? It turns out to be a non trivial task if you're on the wrong track, thankfully I have a teacher at hand to solve the problem in five minutes and make me look incompetent.
So what's the solution? Maybe I'll start with...
The problem:
Find t where t is the vector that shares a common outer tangent with two circles that have centre positions at A and B respectively and radii of R and r.
First we find the vector from A to B (we'll call this vector D for difference), so D = B - A
Using the Pythagorean theory we can at least find out the length of t
But that's not all that helpful, but what we can use is SOH CAH TOA to find omega, we know the Adjacent length (R-r) and the Hypotenuse (|D|) so
(or if you're an idiot like me you'll use arcsin( |t|/|D|) and not notice your gratuitous scheme until you're writing a web-log post on it)
Excellent, now we can find the points P and Q, you also only need to draw one line PQ (or if you want filled in square, PQAB) for each of each circle's neighbours. When the line is drawn from the blue circle it will be on top, and when coming from pink, it will be on the bottom (or vice-versa depending on exact implementation).